A Mathematical Gem Explained With an Elegant Proof

There is so much beauty in mathematics - past the quadratic equations of your horrid algebra class and the tedious long division that seems to be present in every single badly-constructed problem.

There are gems, things that you simply wouldn't believe, that leave people's jaws hanging open thinking that something must be fundamentally wrong with the universe in order to allow for such an insane equality. But most of that doesn't get taught in math classes, because it's "above" the level of most common core math classes. I'm here today to prove that as a falsehood and introduce to you one of the most exciting functions in all of mathematics: $\zeta(s)$

Now, I don't believe I have the ability nor the writing talent to provide a proof of the following that any layperson could understand. So, in this, I'm going to assume a basic knowledge of calculus, including what an integral is, how to integrate, and what sin and cos are.

So - first, let's get a refresher on the cool concept of an "infinite sum". Most people assume that if you add up an infinite amount of positive terms, you will end up with infinity. Well, that's not actually right. Under certain conditions, an infinite sum will slowly come creeping up to a certain number and never surpass it. In that case, we say the infinite sum converges to that number. 

How about an example? Well, let's ask the question, what is the value of the following sum?

$$1+\frac12+\frac13+\frac14+\frac15+\frac16...$$

It turns out the answer is that it blows up to infinity, making the above a bad question. Let's instead look at that same series but with all the denominators squared:

$$1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+\frac{1}{6^2}...$$

Miraculously, it turns out this series converges to a number:
$$\frac{\pi^2}{6}\tag1$$

To me, this is absolutely insane. Pi is the ratio of a circle's circumference to it's diameter, so what is it doing popping up in infinite sums? Well - this blog post is about exactly that. 

So first, let's introduce some notation. Instead of expressing the infinite sum in terms of a few terms and then ellipsis, we have a precise notation:

$$S=\sum_{n=1}^{\infty}\frac{1}{n^2}$$

Let's break this down. Because I know most of the people reading this are going to be programming people, it's like a big for loop or repeat loop. We start with $S=0$, and then we add $\frac{1}{n^2}$ to it for $n=1$ (which is why the bottom of the sum says $n=1$). Then, we add $\frac{1}{n^2}$ to it for $n=2$. Then for $n=3$. And so on, all the way to infinity. 

And we don't have to just square the number. We're interested in raising it to every power. In general, that sum with the denominator raised to the $s^{th}$ power is called $\zeta(s)$. We are going to talk about $\zeta(2)$. 

Now that we have introduced the notation, how do we actually prove our original theorem $(1)$? Well, here is the hard part. I will now introduce the concept of a Fourier Series. A Fourier series is a way of approximating a function in a certain range as a sum of sines and cosines. Let's say we have the graph of $x^2$ between $-\pi$ and $pi$. Call this $f(x)$. We can then, using a Fourier series, create an infinite sum that models this curve exactly. This infinite sum will be the sum of $\cos(x*n)$ multiplied by the nth term of $a$ (a is a list of numbers) plus  $\sin(x*n)$ multiplied by the nth term of $b$ (b is also a list of numbers). That whole infinite sum will then be added to the first term of $a$ (actually the zeroth term, 'cause we index from zero like real men) over 2. Expressed using our notation:

$$\dfrac{a_{0}}{2}+\sum_{n=1}^{\infty }(a_{n}\cos nx+b_{n}\sin x)$$ 

So, the problem is finding what the nth term of a and b is. 

Well, thanks to the man himself (Fourier), we know that:

$$a_{n}=\dfrac{1}{\pi }\int_{-\pi }^{\pi }f(x)\cos nx\;dx\qquad n=0,1,2,3,...,$$ 

$$b_{n}=\dfrac{1}{\pi }\int_{-\pi }^{\pi }f(x)\sin nx\;dx\qquad n=1,2,3,... .$$ 

The graph of the integrand of $b_n$ looks like this:

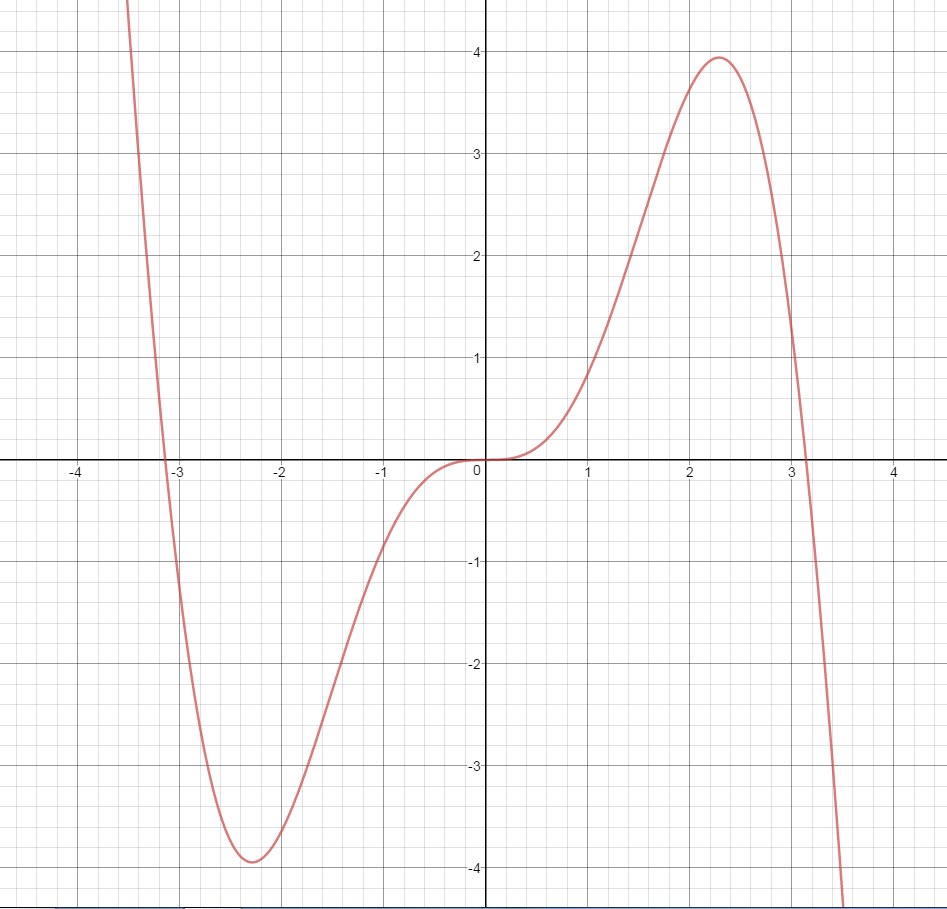
The lines intersect y=0 at our integral bounds, and recalling that the definition of the integral is the area under the curve, since the curve is mirrored on both sides of the x axis, they cancel out which means $b_n$ is always 0. This reduces our equation to:

$$\dfrac{a_{0}}{2}+\sum_{n=1}^{\infty }(a_{n}\cos nx)$$ 

So all we  have to do is integrate $a_n$. This can be done by changing the integral bounds to 0, Pi, observing the antiderivative of the integrand and evaluating at the limits. For a more in-depthh explanation of how to integrate, just message me on whatever platform you know me from or at my email. 

But, in the end, we get:

$$a_{n}=(-1)^{n}\dfrac{4}{n^{2}}$$

Excluding the special case of $a=0$, which can be easily integrated to be $\frac{2\pi^2}{3}$.

Thus

$$f(x)=\dfrac{\pi ^{2}}{3}+\sum_{n=1}^{\infty }\left( (-1)^{n}\dfrac{4}{n^{2}}\cos nx\right) .$$

Remembering that $f(x)=x^2$, which is the function we just found the fourier series of,  $f(\pi )=\pi ^{2}$, plugging in $\pi$ for x, we obtain

$$\pi ^{2}=\dfrac{\pi ^{2}}{3}+\sum_{n=1}^{\infty }\left( (-1)^{n}\dfrac{4}{n^{2}}\cos \left( n\pi \right) \right) $$ 

Extracting the constant 4 from the sum and simplifying:

$$\pi ^{2}=\dfrac{\pi ^{2}}{3}+4\sum_{n=1}^{\infty }\left( (-1)^{n}(-1)^{n}\dfrac{1}{n^{2}}\right) $$

$$\pi ^{2}=\dfrac{\pi ^{2}}{3}+4\sum_{n=1}^{\infty }\dfrac{1}{n^{2}}.$$

Therefore

$$\sum_{n=1}^{\infty }\dfrac{1}{n^{2}}=\dfrac{\pi ^{2}}{4}-\dfrac{\pi ^{2}}{12}=\dfrac{\pi ^{2}}{6}$$

It always is so baffling how you think such a result is so impossible, but then just show, with cold hard logic, that it must be true. It seems insane, but it's true. I am sorry that I sort of jumped around in difficulty levels, if you need further clarification on something feel free to contact me via email, Twitter, Hopscotch forum, or whatever. Thank you so much for reading through, and I'll see you in the next (less math-y) post! :D